Business Mathematics
Chapter 1 : Matrices & Determinants
EXERCISE
1 (c) i specifies the rows in which the element appears 2 (c) Both A and B 3 (b) A single row and nay number of columns 4 (a) below the main diagonal are zeroes 5 (a) They have the same order 6 (d) a × d 7 (c) 8 (d) A’A = I 9 (a) 125 10 (c) 11 (c) Negative of the value of the original determinant 12 (d) 100 13 (a) A unique solution 14 (b) Only one trivial solution 15 (b) 16 (c) total requirement of each spare part at each of the branch. 17 (b) 18 (b) Positive
PREVIOUS YEARS’ QUESTIONS
1 (c) |A| = 0 and (adj. A) B = 0 2 (a) total amount spent by X and Y on purchase of three flavours 3 (c) positive 4 (a) Commutative 5 (c) 6 (c) 7 (d) 8 (d) The system has its determinant, i.e., |A| = 0 and (adj A) B is not equal to zero 9 (b) Infinite many non-trivial solutions 10 (c) 11 (a) 12 (d) 13 (c) Production level of an industry is determined on the basis of certain optimality criteria 14 (a) Determinant of Leontief matrix (I – A) must always be positive and aij for i = j should be less than one. 15 (a) Identity matrix 16 (a) – A 17 (d) 60 18 (a) m × n 19 (c) Agriculture sector – 1333 units, Industry sector – 1000 units, 1133 hrs. 20 (d) Rs. 330 21 (a) 0 22 (a) 60, 90 23 (c) 3 24 (b) 10/3
Chapter 2 : Linear Programming
EXERCISE
1 (c) The table is the final table of the simplex algorithm as it shows the case of unbounded solution. 2 (a) The given problem has an alternate solution. 3 (a) Set of all points for which non-negativity condition is satisfied. 4 (c) Slack, surplus and artificial variables. 5 (d) All of these 6 (b) Surplus variable 7 (c) Negative 8 (a) Multiple optimal solutions 9 (c) Equal to 10 (c) Non-negative 11 (a) A slack variable 12 (c) 13 (b) Infeasible solution 14 (a) Same 15 (c) Objective function
PREVIOUS YEARS’ QUESTIONS
1 (d) unique optimum solution 2 (b) basic feasible solutions 3 (b) 4 (b) 5 (a) Slack variable 6 (c) (m – n) 7 (c) degenerate solution 8 (a) constraints 9 (b) A subjective function 10 (b) Resource is not fully utilized 11 (a) multiple optimal 12 (d) A possible solution on the graph corresponds to every point (x, y) 13 (b) An infeasible solution 14 (a) Imputed value of the resources 15 (b) Iso-cost line coincides with a constraint line 16 (a) Cj – Zj > 0 17 (d) Minimize the costs of nutrient blends 18 (a) Infeasibility 19 (c) By choosing the variable which yields the minimum positive ratio of quantity to substitute rate in the key column 20 (d) The constraints are inconsistent and feasible region does not exist 21 (d) Basic variables 22 (a) Solution by a simplex method requires that all the constraint of a given LPP have none of the constants of the constraints with negative sign 23 (b) Basic variable has value equal to zero 24 (c) Use of available resources 25 (d) Linear programming is probabilistic in nature. 26 (b) An infeasible solution 27 (c) It is always necessary to convert inequality constraint into equality constraint for writing dual of an LPP. 28 (*) 29 (b) Maximize 120 T + 80 C 30 (c)
* If the amount spent is Rs.100 instead of Rs.10 then the answer is B. Otherwise the correct answer is not given in the options.
Chapter 3 : Functions, Limits & Continuity
EXERCISE 1
1 (c) 16 2 (a) 11 3 (b) 2 4 (c) 5 (c) 900 6 (a) 7 (b) 8 (c) 0 9(c) x = 20p 10 (d) 10, 35 11 (b) x = 146, p = 77 12 (c) x = 3, p = 3
EXERCISE 2
1 (b) 12 2 (b) 1/4 3 (a) 1/5 4 (d) 6 5 (d) None of these 6 (b) a = 2, l = 3 7 (d) does not exist 8 (b) 48 9 (b) 4 10 (a) 2 11 (a) 2 12 (b) 13 (c) 14 (c)2 15 (a) 1/3 16 (b) 2/3 17 (b) -2/5 18 (a) 0
EXERCISE 3
1 (b) x = 1, x = 2 2 (b) Discontinuous at x = 0 3 (b) 2 4 (c) Continuous at x =2 5 (c) β = 0, α is any real number 6 (b) -1 7 (*) 8 (b) Discontinuous at x = 0 9 (b**) for x = 1 10 (b) -2
* wrong question
** The modified question:
If f(x) = {The given function definition} then x is Continuous:
PREVIOUS YEARS’ QUESTIONS
1 (c) 2/3 2 (b) 6 3 (c) 100 4 (b) x = 1 5 (b) -23 6 (d) 2000 7 (c) Rational function
Chapter 4 : Differentiation
EXERCISE
1 (a) 27 2 (b) 100 3 (c) 10 4 (b) 4 5 (c) 40 6 (a) 50 7 (a) 8 (b) 12 9 (d) 2000 10 (a) 17 11 (a) Decrease 12 (a) q = 18 13 (c) slope of average cost (MAC) 14 (d) equilibrium state which will automatically adjust both the price and the quantity in the market. 15 (c) minimises total cost of inventory 16 (b)
PREVIOUS YEARS’ QUESTIONS
1 (d) upward sloping function 2 (b) elastic 3 (c) 4 (c) Slope of MR = 2(Slope of AR) 5 (a) 150 6 (d) 6 7 (b) 26 8 (d) 6 9 (d) 0.01x-0.02-(5000/x2) 10 (b) 8 – (x/125) 11 (a) (2/5) 12 (d) 100 months 13 (b) 500 units 14 (c) x 15 (d) 16 (c) Average variable cost is minimum 17 (b) 150 18 (a) 70 19 (b) 20 (b) increasing and convex from below 21 (c) Inelastic 22 (b) x = 40 23 (b) P1 < P2 24 (c) Certain and uniform demand with zero lead time 25 (a) Decrease 26 (b) Unit elastic then x = 1 27 (a) q = 18 28 (c) Same as in Market II 29 (a) 30 (b) 12 31 (a) 17 32 (d) 33 (b) x = -1 34 (d) 240 35 (****) 36 (d) 2-(x\y) 37 (b) 400
* Wrong question.
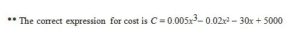
*** Wrong Question
Chapter 5 : Partial Differentiation
EXERCISE
1 (a) Decreasing 2 (b) Constant 3 (d) (HK – HL) / (HL – BK) 4 (d) 51 5 (b) elasticity of output 6 (a) non-homogeneous production function
* Correct Answer = 51.
PREVIOUS YEARS’ QUESTIONS
1 (c) Homogeneous production function of degree α + β 2 (a) Complementary 3 (d) 150 4 (b) constant 5 (a) Decreasing 6 (c) 3 and has increasing returns to scale 7 (c) AC – B 2 > 0 8 (a) e11 and e22 are negative, and e12 and e21 positive 9 (b) Increasing returns to scale 10 (c) AC – B2 = 0 11 (d) Homogeneous function of degree –1 12 (b) Both cross partial elasticities are negative 13 (a) Ratio of proportionate change in factor ratio of the proportionate change in MRTS 14 (d) Constant product curves are downward sloping and convex to origin 15 (c) Constant product curves are upward sloping 16 (b) Double of the total output 17 (c) 1.1
Chapter 6 : Integration
EXERCISE
1 (a) P = 54x – (9/2)x2 – 121.50 2 (a) 3 (c) 88/3 units 4 (c) 11 – (1/3)x3 5 (b) 72
PREVIOUS YEARS’ QUESTIONS
1 (c) 2 (c) 0.001X3 – 0.3X2 + 30X + 42 3 (a) 9 -(4/3)X2 4 (b) 100 5 (a) 8 6 (a) 7/2 7 (c) C= 4x – x2 + (x3/3) + 100 8 (b) p = 2 – 3x 9 (a) 8 years, 16 millions rupees 10 (d) p = 11 – (x3/3) 11 (d) 576 12 (c) 72 13 (a) C = 2000 e0.001x 14 (b) 27 15 (c) 32/3 16 (d) 576 17 (b) 10x – 3x2 18 (d) 27 19 (c) 28.58 20 (d) 21 (b) 1.0
* Correct answer = 32/3
Chapter 7 : Mathematics of Finance
EXERCISE
1 (b) annuity of size P continues forever. 2 (c) 5.8% 3 (c) 20% 4 (b) 3.02% 5 (b) 0.04 6 (d) Rs.8925 7 (b) Rs.3 8 (d) 6.09% 9 (b) the annuity size to accumulate the sum of money S over n time intervals 10 (d)
PREVIOUS YEARS’ QUESTIONS
1 (c) 2 (a) the annuity size 3 (a) 12,500 4 (b) 10% 5 (d) 8.16% 6 (b) 8% 7 (d) None of these 8 (d) Compounding is continuous 9 (c) d 10 (b) Annuity of size P continues forever 11 (a) 22.7% 12 (a) 6.09% 13 (c) The first payment of which is made at the beginning of the first payment interval 14 (a) Rs. 50,000 15 (b) 16 (a) Ordinary 17 (c) 18 (b) 0.04 19 (d) Rs. 8925 20 (b) Rs. 3 21 (d) 6.09% 22 (d) 612 23 (d) Annuity Fund 24 (d) Rs. 6,845.80 25 (d) 9.52% 26 (b) 10 27 (a) Rs. 25000 28 (a) 20 year 29 (a) 7974.8 30 (d) A = P (1 + i)n

